My local supermarket runs a campaign where you can collect stickers for a photo album 📔 with historic pictures of our pitoresk town. For every 10 euros you get a package of 4 stickers and in total there are 229 unique stickers. My question is:
How many stickers including doubles do you need to get a full album? 💁
This is known as the Coupon collector’s problem (a variant of the birthday problem). The first card you will always have a new unique card. The change that the second card is a new unique card is $1$ minus the change that you have the same card as the first:
$$p = 1 - \frac{1}{n} = \frac{n-1}{n}$$
When you already collected $i$ unique stickers; the change that you get a new unique card is:
$$p_i = \frac{n-i}{n}$$
The expected number of stickers to get a _new unique card is:
$$t_i = \frac{1}{p_i} = \frac{n}{n-i} $$
The expected number of stickers required to get the full album of unique stickers is the total sum:
$$T = t_0 + t_1 + … + t_{n-1} = \sum^{i=0}_{n-1} \frac{n}{n-i}$$
>>> sum([229 / (229 - i) for i in range(229)])
1377.0043621760467
With 1377 stickers (345 packages and euro 3450 spent 💶) there is a 50% change that you have a full album.
Monte Carlo simulation
To get an idea of the variance I ran a Monte Carlo simulation with 10.000 runs that resulted in an average of 1376.6421 cards to complete the album (which I probabbly won’t achieve).
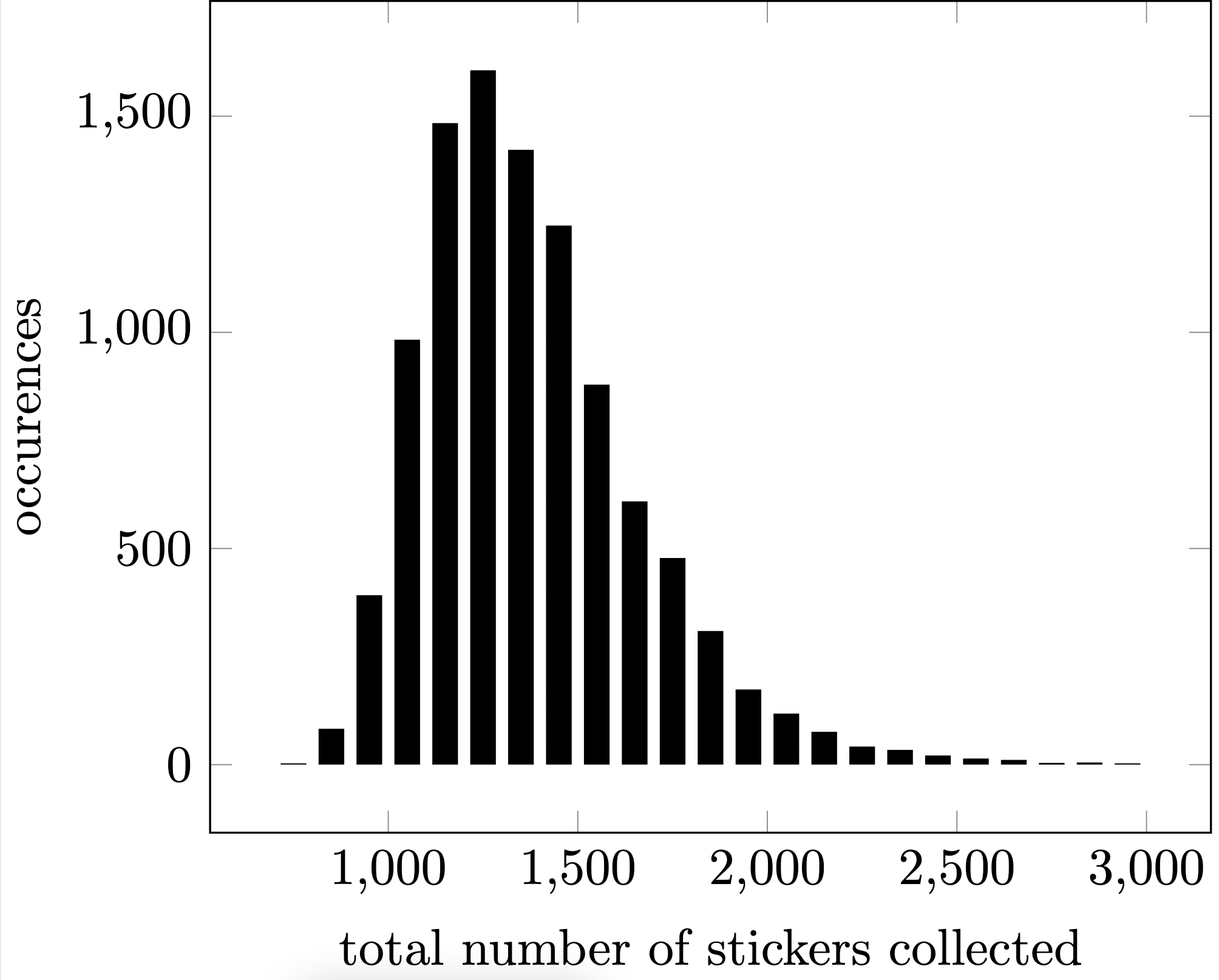
# Monte Carlo
from random import randint
def get_a_full_collection(n):
cards = []
while len(set(cards)) < n:
cards.append(randint(1, n))
return len(cards)
results = [get_a_full_collection(229) for _ in range(10000)]
Update 24th January
Now I have 65 packages, so 260 stickers, collected. Of the 229 unique stickers I already have collected 133. Expectation is to require only 200 stickers to reach 133 uniques; I am doing really bad in my collection journey.