I am often a DIY’er and I have a really heavy hatch (32 kg) at home that I want to open automatically with an electric actuator. Something like the hatch in the image below.

You can buy these actuators for 50 to 100 euros online: but which one do I need? or:
- What is the minimal and maximal length (and stroke) that I need?
- What is the force the actuator should be able to push?
I made a schematic model, with
- $l$ is the length of the hatch ($l=0.75 m$ in my situation)
- $a$ and $b$ are yet unknown attached positions of the actuator from the hinch
- $\varphi$ is the the angle of the hatch between 0 and 90 degrees
- $\theta$ is the angle of the actuator with the vertical $\theta$
- $w$ is the dynamic actuator length, dependant on the hatch position.
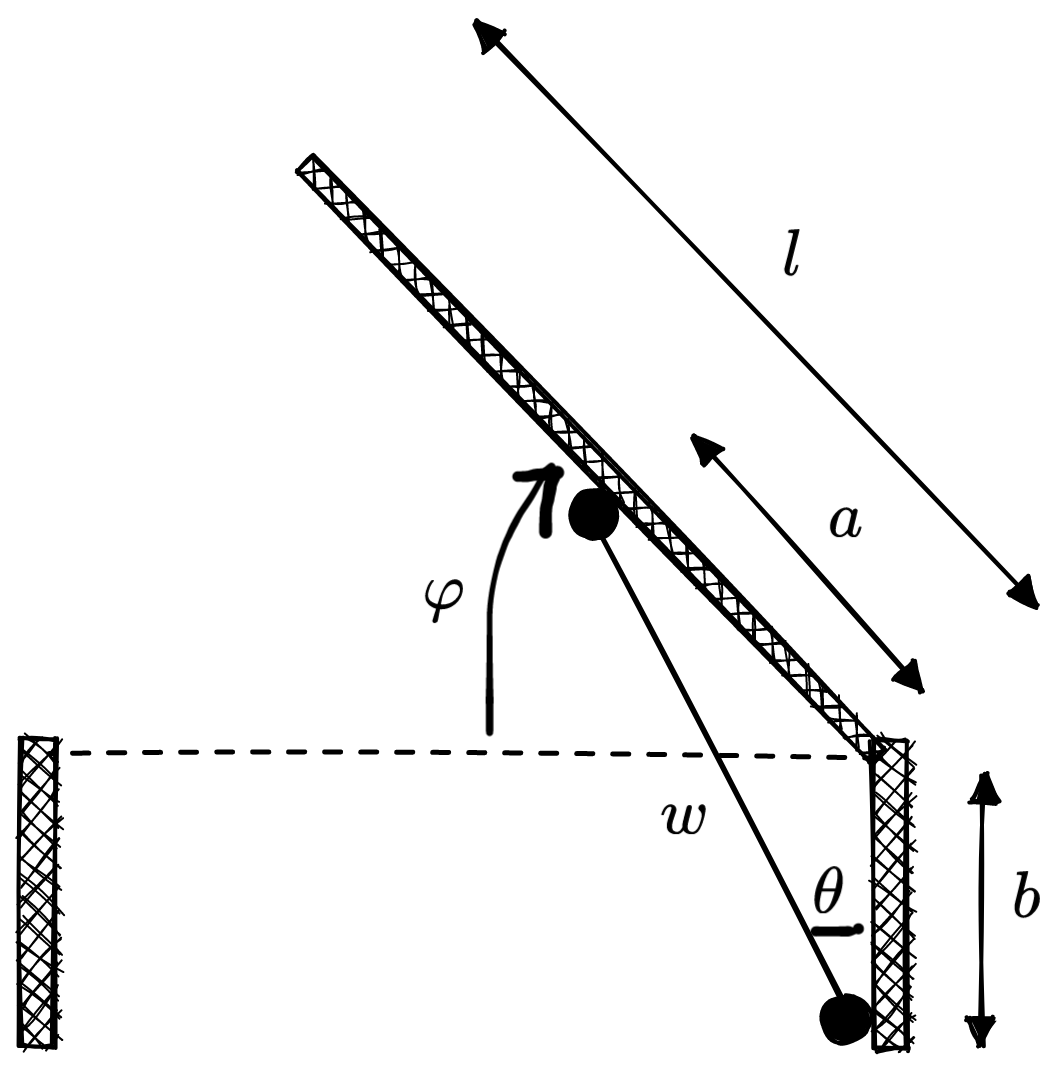
Actuator length
With some geometry and pytagorasch we can calculate $w$ dependant on hatch position:
$$w^2 = \left(a\cdot\sin\varphi+b\right)^2+\left(a\cdot\cos\varphi\right)^2$$
From which follows that $w$ varies between the retracted length:
$$(\varphi = 0) \rightarrow w_\text{retracted} = \sqrt{a^2+b^2}$$
and the extended length:
$$(\varphi = 90) \rightarrow w_\text{extended} = a+b$$
The minimal stroke length is the difference:
$$\Delta w = a+b-\sqrt{a^2+b^2}$$
Force on the actuator
The weight of the complete hatch is $W = m \cdot g = (32) \cdot (10) = 320 N$. From the moment around the hinge, you can calculate the normal force on the actuator:
$$F_x = \frac{Wl}{2a \cdot \cos \theta}$$
Which shows that the force in the actuator is the largest where $\theta$ is the smallest, which is when the hatch is closed ($\theta=0$). With some more geometry we find the relation between $\theta$ and $\varphi$ as:
$$\tan \theta = \frac{a \cdot \cos \varphi}{a \cdot \sin \varphi+b}$$
So the maximum force is where:
$$\tan \theta = \frac{a}{b}$$
Then simplify, with $\cos \left(\arctan (x)\right) = \frac{1}{\sqrt{x^2+1}}$; we can rewrite the solution for the maximum force to:
$$F_{\text{max}} = \frac{Wl}{2} \sqrt{\frac{1}{a^2}+\frac{1}{b^2}}$$
Choose a product
Luckely, there are many suppliers. As a ballpark figure, when $a=0.35m$ and $b=0.25m$:
- $w_\text{retracted} = 0.43m$
- $w_\text{extended} = 0.60m$
- $F_\text{max} = 590 N$
Here a list of products that meet my requirements
| Item | Price | $w_\text{retracted}$ | $w_\text{extended}$ | $F_\text{max}$ | speed |
|---|---|---|---|---|---|
| DD 300 mm | €88 | 420mm | 720mm | 700N | 20 mm / sec |
| DD 400 mm | €119 | 550mm | 950mm | 700N | 20 mm / sec |