While skiing in the Swiss Alps last winter, I got into a discussion about speed. Following my engineering knowledge, your skiing speed does not depend on your own mass. Without the intention to offend anyone, skiing is basically a form of falling at an angle.

basic skier model

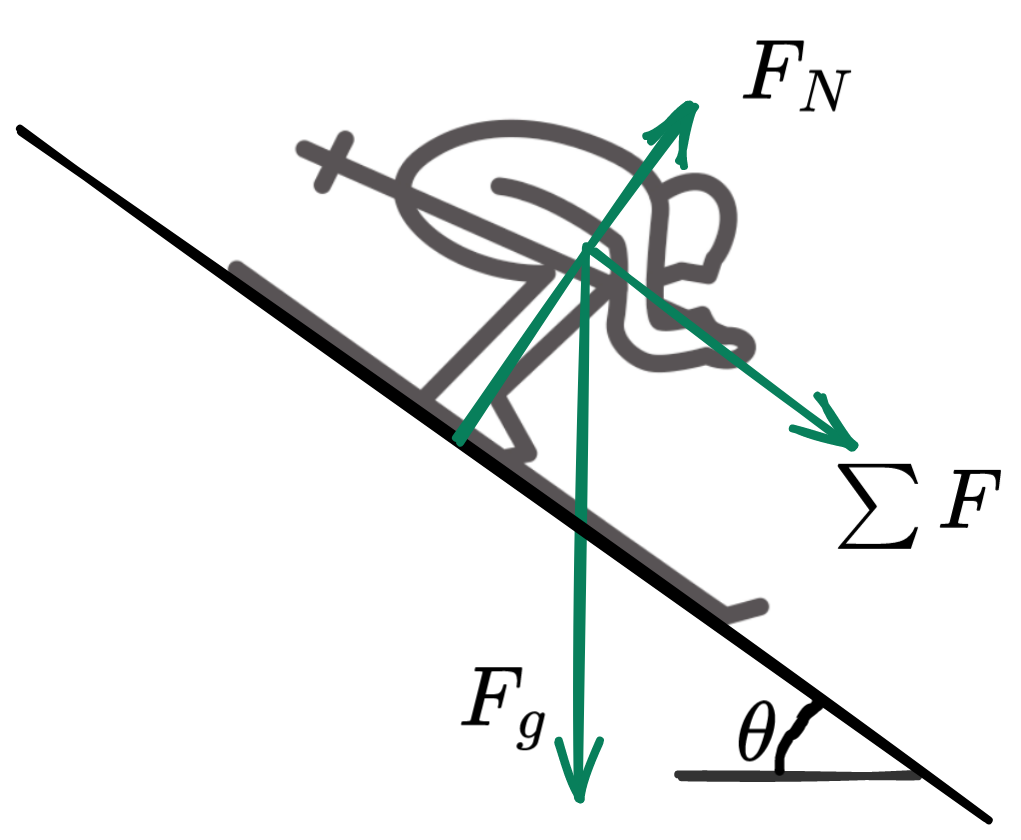
We can build a model based on Newton’s second law where acceleration times mass is equal to the resultant force. We can see that mass ($m$) will drop out of the equation:

$$ \begin{aligned} \sum F = m \cdot a &= m \cdot g \cdot \sin \theta \cr a &= g \cdot \sin \theta \end{aligned} $$

Here $a$ is the acceleration of the skier, $g$ is the gravitational acceleration and $\theta$ is the angle of the slope or piste with the horizontal.

This was already demonstrated by Simon Stevin and Jan Cornets de Groot in 1586 or Galileo around 1589 both with free-falling objects from a classical tower.

This may feel counter intuitive…

But is it true?

In the above case we neglect all friction of which, in case of skiing, there are two:

  • Kinetic friction or sliding friction; the friction between your skies and the snow, it is proportional to your own mass and therefore does not make your speed dependent on mass 😌

  • Drag or air resistance; friction between your body/posture and the air and is completely independent of your mass; here is the devil! 🔥

What is actually the contribution of drag? And if it is significant, can we apply a simple factor to speed to compensate for mass? Lets check it!

Equation time

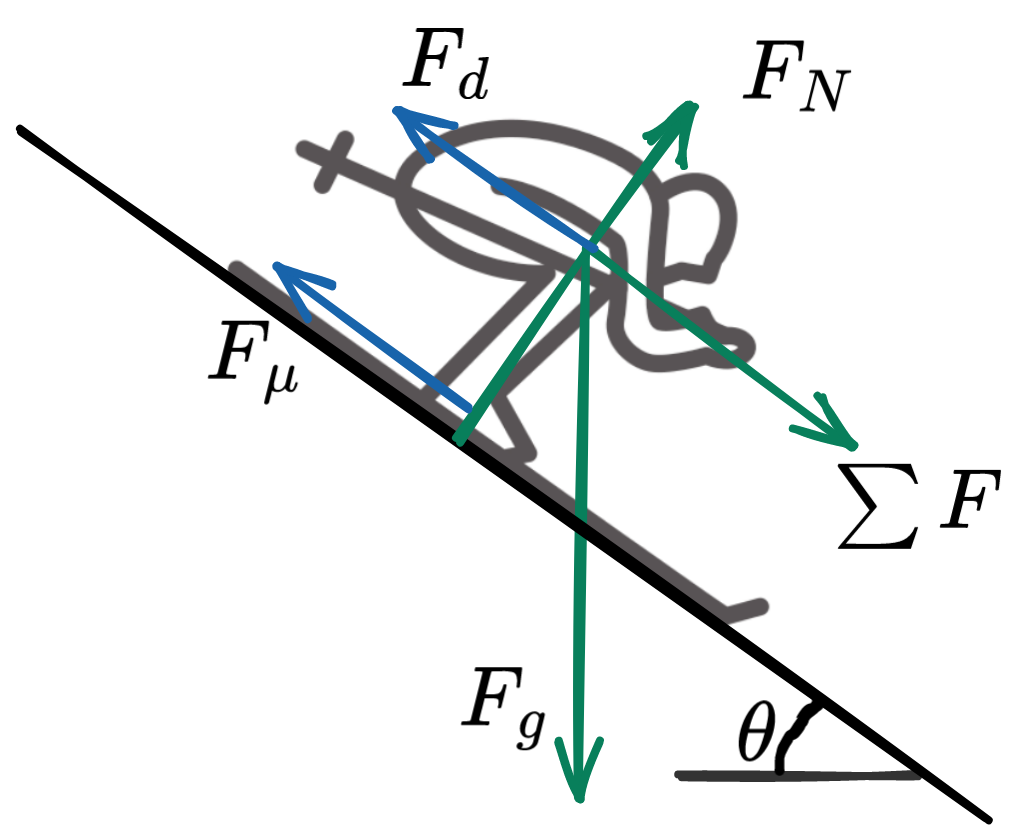
I’ll start by setting up the full equation of motion including friction and drag.

  • Kinetic friction equals a coefficient ($\mu$) times the force normal to the ground: $$F_\mu= \mu mg \cos \theta$$ The coefficient depends on many things and you can find a couple of studies on it, for example this detailed study from 1988. I think assuming a constant value of $\mu=0.04$ would be alright.

  • Drag depends on the frontal surface area ($A$) of the skier, the air density ($\rho$), a drag coefficient ($C_d$) and the squared speed ($v$) : $$F_d= \frac{1}{2} \rho A C_d v^2$$ Drag is always in the opposite direction of the movement. There are many ways how a skier can influence the frontal surface area and the drag coefficient with different positions; so this is where skills come into the game! We’ll go with something like $\rho=1.204$ $kg/m^3$, $A=0.28$ $m^2$ and $C_d=0.63$.

Put together and we get a differential equation for $v>0$ $m/s$:

$$m\frac{\partial v}{\partial t} = m g \left(\sin \theta - \mu \cos \theta \right) - \frac{1}{2} \rho A C_d v^2$$

basic skier model

Life is simple

Don’t worry; this equation on an endless straight piste (the angle $\theta$ is a constant) is not too hard too solve when you have YouTube.

With the following two constants $$ j= g \left(\sin \theta - \mu \cos \theta \right)$$ and $$k=\frac{\rho A C_d}{2 m} $$

We can rewrite the differential equation for $t \geq 0$ as:

$$\frac{\partial v}{\partial t} = j - k v^2$$

…move the partials around…

$$\partial t = \frac{\partial v}{j-kv^2}$$

…integrate both sides…

$$ \begin{aligned} t &= \int^v \frac{\partial v}{j-kv^2} = \frac{1}{j}\int^v \frac{\partial v}{1-(\sqrt{k/j}\cdot v)^2} \cr & = \frac{1}{\sqrt{kj}} \tanh^{-1} \left( \sqrt{k/j} \cdot v\right) \end{aligned} $$

…and reorganize to get our solution:

$$v(t) = \sqrt{\frac{j}{k}} \tanh \left( \sqrt{kj}\cdot t \right)$$

Since $\tanh$ converts to 1; we can derive that the speed will convert to a maximum:

$$v_{\max} = \sqrt{\frac{2 m g \left(\sin \theta - \mu \cos \theta \right)}{\rho C_d A}}$$

The maximum speed is proportional to the square root of the mass.. if person A is 64 kg and person B is 100 kg, person B would be $\sqrt{100/64}=1.25$ times faster!

So finally… we will have a fair race when everyone’s clock time is multiplied by the following factor:

$$f_m = \sqrt{\frac{m}{100}}$$

Not too fast

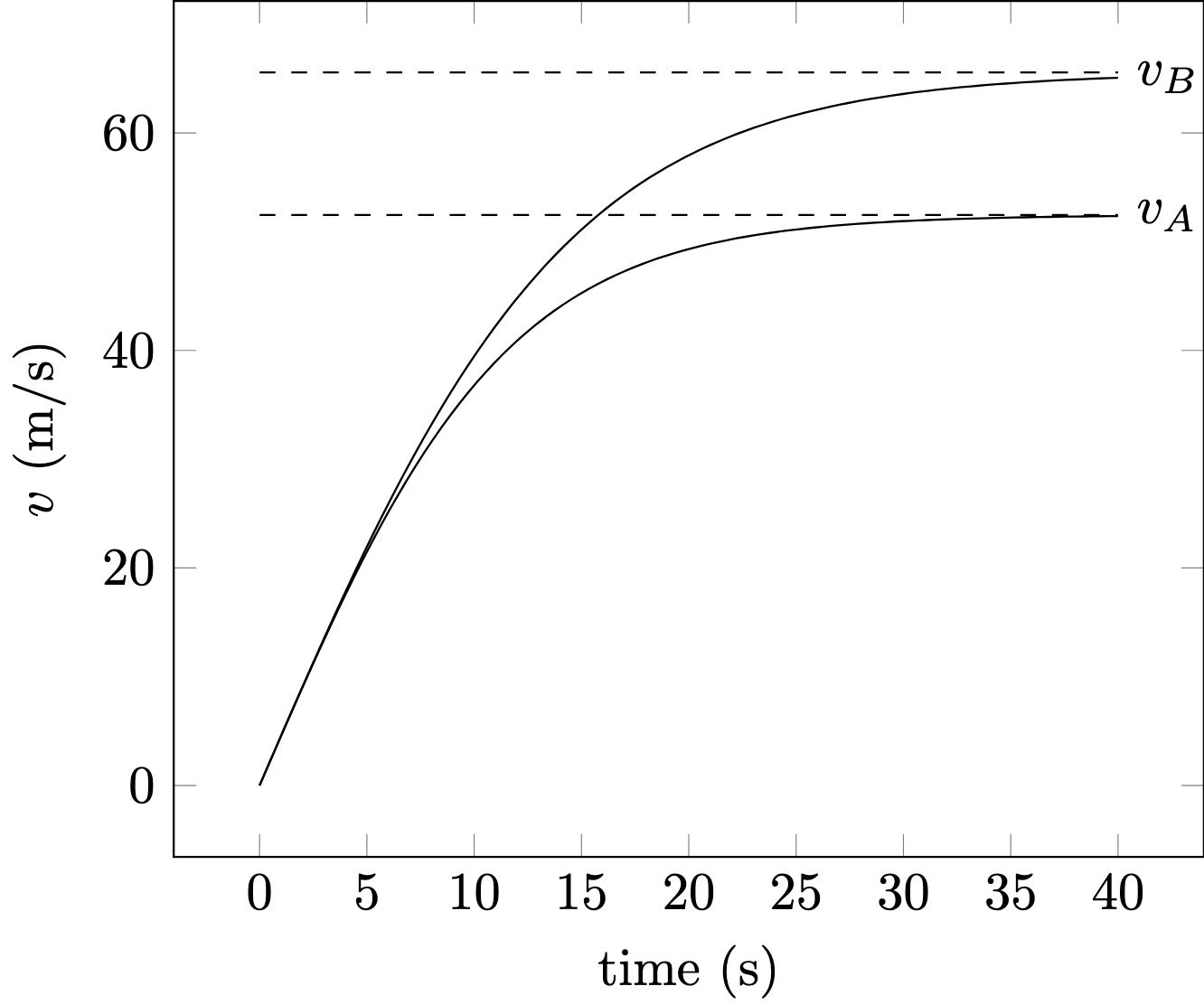
Although the maximum speed has a calculable ratio, depending solely on the mass, this does not apply to the speed in the acceleration phase. There is a $\sqrt{1/m}$ inside the $\tanh$; so with more mass it will take longer before the maximum speed is reached.

When we plot the speed in time, we see the ratio $v_A/v_B$ will gradually drop from 1 to 0.8.

basic skier model velocity

distance

Since a race has to cover a certain distance, can we find a calculable ratio here?

To know the distance that a skier has covered in a certain time, we integrate over time:

$$ \begin{aligned} s & = \int v \partial t = \sqrt{\frac{j}{k}} \int \tanh \left( \sqrt{kj}\cdot t \right) \partial t \cr & =\frac{1}{k} \ln \left( \cosh \left( \sqrt{kj}\cdot t \right) \right) \end{aligned} $$

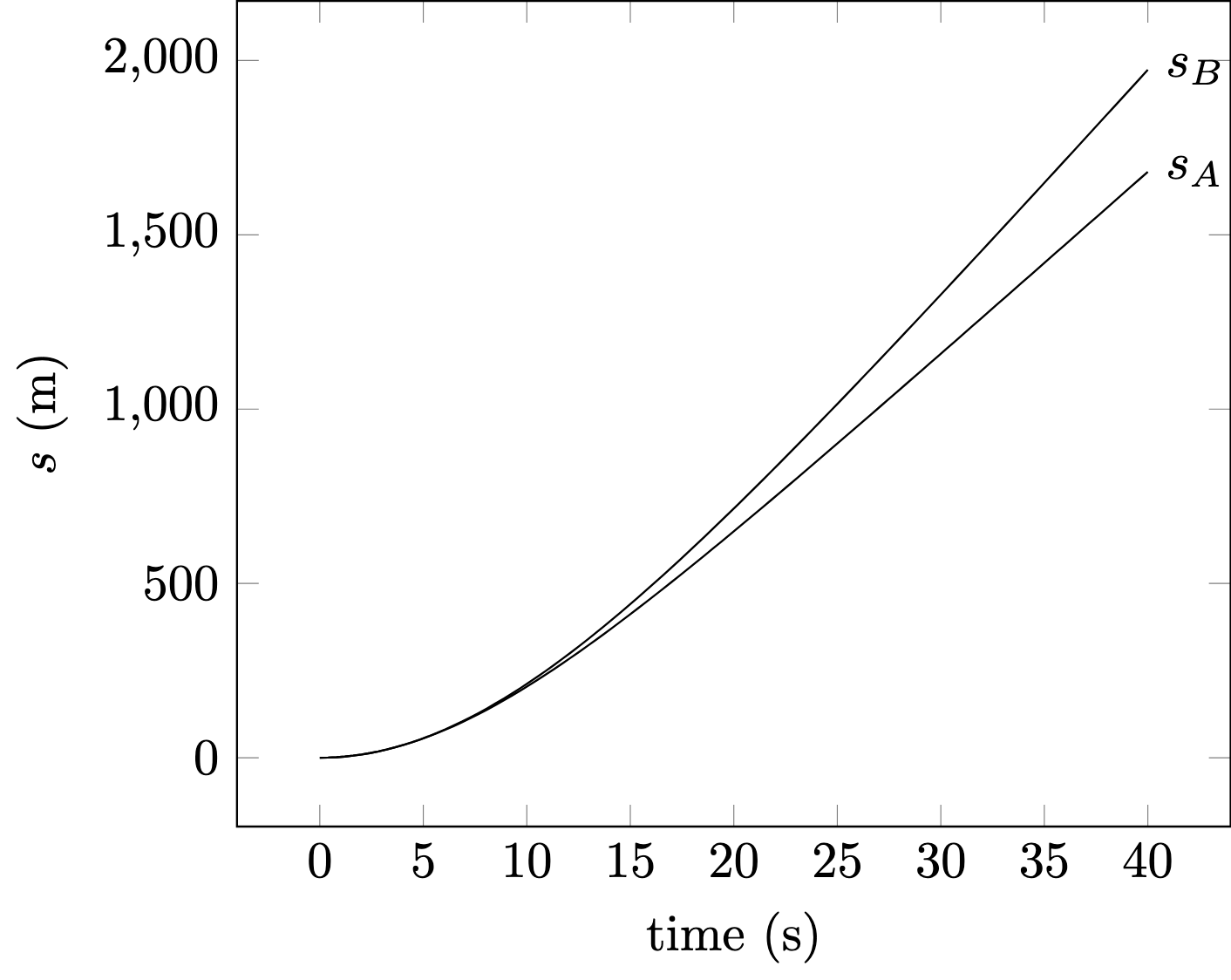
and this we can plot for skier A and B:

basic skier model distance

You can reorganize the equation to estimate the time it takes to cover distance $s$:

$$ t = \frac{1}{\sqrt{kj}}\cosh^{-1} \left( e^{sk} \right) $$

But back to the point.

Because the mass is in two different places in the distance equation; it is not easy (at least for me) to calculate a ratio that depends only on the mass.

If we look at the distance ratio $s_A/s_B$ over time:

basic skier model distance

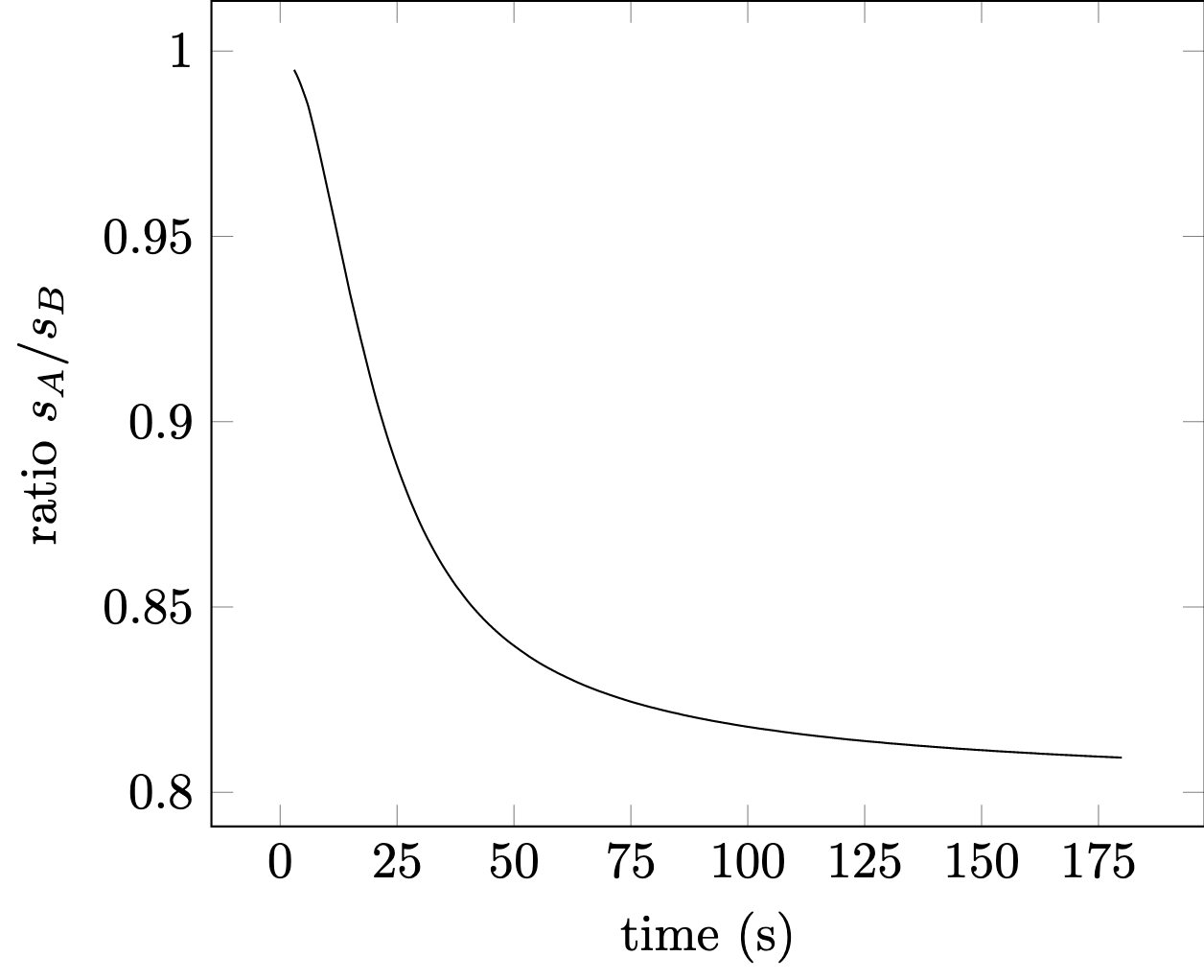
we can conclude:

  • that mass certainly results in a higher velocity
  • over a longer distance the ratio can be estimated with $f_m$

Some marginal notes:

  • this is really skiing without making any turns, I know
  • a realistic slope is probably not at a constant angle; maybe I’ll check some other time what the effect of that would be